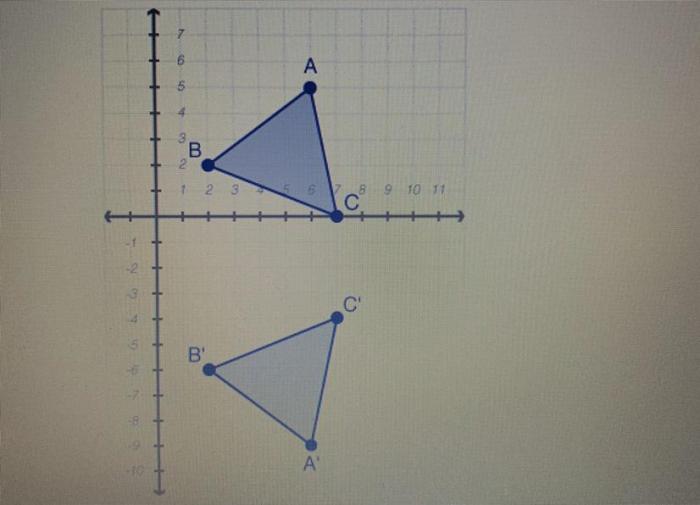
Triangle abc was reflected over line m – In the realm of geometry, the reflection of triangle ABC over line m unveils intriguing transformations that reshape its characteristics and open doors to practical applications. This exploration delves into the process, properties, and significance of triangle reflection, providing a comprehensive understanding of this fundamental concept.

When triangle ABC undergoes reflection over line m, its image emerges as a mirror image across the line. This transformation preserves the triangle’s shape and size, while altering its orientation relative to the line of reflection.

1. Introduction

Triangle reflection is a geometric transformation that creates an image of a triangle by flipping it over a line. The original triangle is called the pre-image, and the resulting image is called the reflected triangle. The line over which the triangle is reflected is called the line of reflection.

Analyzing the reflection of triangle ABC over line m helps us understand the properties of the reflected triangle and how it relates to the pre-image.

2. Reflection of Triangle ABC over Line m

To reflect triangle ABC over line m, we draw perpendicular lines from each vertex of the triangle to line m. The points where these lines intersect line m are the corresponding points of the reflected triangle. We then connect these corresponding points to form the reflected triangle.

The resulting image of triangle ABC after reflection is a triangle that is congruent to the original triangle. This means that the reflected triangle has the same shape, size, and orientation as the pre-image.

3. Properties of the Reflected Triangle

The reflected triangle has several properties that are related to the pre-image:

• The corresponding vertices of the reflected triangle are equidistant from the line of reflection.
• The corresponding sides of the reflected triangle are parallel to the corresponding sides of the pre-image.
• The corresponding angles of the reflected triangle are congruent to the corresponding angles of the pre-image.

4. Applications of Triangle Reflection

Triangle reflection has several real-world applications, including:

• Architecture: Triangle reflection is used in the design of buildings and other structures to create symmetrical and aesthetically pleasing designs.
• Computer graphics: Triangle reflection is used in computer graphics to create realistic images and animations.
• Engineering: Triangle reflection is used in engineering to analyze the forces and stresses on structures.

5. Advanced Concepts



Triangle reflection can be extended to more advanced concepts, such as:

• Reflection in multiple dimensions: Triangle reflection can be performed in multiple dimensions, such as in 3D space.
• Reflection of non-Euclidean triangles: Triangle reflection can be applied to non-Euclidean triangles, such as spherical triangles.
• Applications of triangle reflection in computer graphics and animation: Triangle reflection is used in computer graphics and animation to create realistic images and animations.

Essential Questionnaire: Triangle Abc Was Reflected Over Line M

What is the purpose of analyzing the reflection of triangle ABC over line m?

Analyzing the reflection helps us understand how the triangle’s properties change and how the reflection affects its position and orientation relative to the line of reflection.

How does the reflection affect the triangle’s vertices, sides, and angles?

The reflection preserves the lengths of the sides and the measures of the angles, but it changes the positions of the vertices, creating a mirror image across the line of reflection.